¿Cómo son las ecuaciones de movimiento para un sistema de dos resortes y una masa con gravedad en el formalismo de Newton? (Resortes en serie)

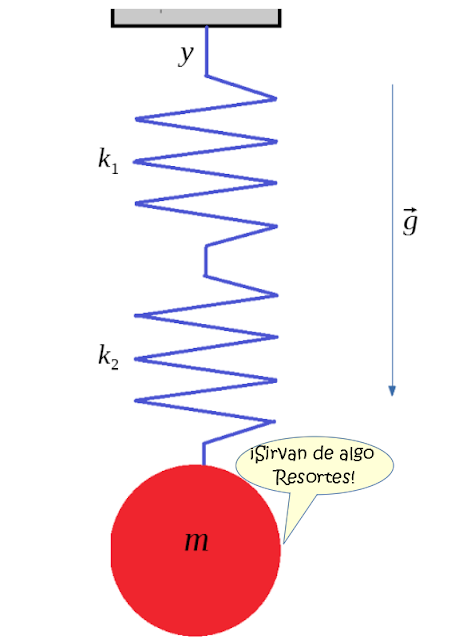
Como me gusta complicar un poco más los problemas, ahora a los dos resortes vistos anteriormente, les vamos a agregar atracción gravitacional:

La sumatoria de fuerzas para este problema de acuerdo a la ley de Hooke para cada resorte:

\[\sum F_{y}: ma=-k_{1}y_{1}-k_{2}y_{2}\]

Como ambos resortes, se ven afectados por la misma fuerza de la masa $m$, los resortes se comprimen y/o alargan a una distancia $y_T$ (distancia total), que viene representado por la suma de las distancias que recorre cada resorte:

\[y=y_1+y_2\]

Y de acuerdo a la ley de Hooke, $F=-ky$, es posible despejar la distancia recorrida $y=-\frac{F}{k}$, tenemos en cuenta que en cada resorte actúa la misma fuerza ejercida por la masa:

\[-\frac{F}{k_e}=-\frac{F}{k_1}-\frac{F}{k_2}\]

\[\frac{1}{k_e}=\frac{1}{k_1}+\frac{1}{k_2}\]

Sumando podemos obtener el valor de la constante del resorte equivalente $k_{e}$ en términos de $k_1$ y $k_2$:

\[\frac{1}{k_e}=\frac{k_1+k_2}{k_{1}k_{2}}\]

\[k_{e}=\frac{k_{1}k_{2}}{k_1+k_2}\]

así la suma de fuerzas en términos de la constante del resorte equivalente será:

\[\sum F_{y}: ma=-k_{e}y+mg\]

Podemos obtener una ecuación de movimiento y una solución análoga, al oscilador armónico unidimensional con gravedad:

\[\ddot{y}+\frac{k_e}{m}y=g\]

\[y(t)=Asen(\omega_{e}t+\phi)+\frac{g}{\omega_{e}^{2}}\]

Donde $A$ es la amplitud, $\omega_{e}=\sqrt{\frac{k_{e}}{m}}=\sqrt{\frac{k_{1}k_{2}}{(k_1+k_2)m}}$ la frecuencia angular en términos de las constantes de los resortes, $t$ el tiempo, y $\phi$ el ángulo de fase.

La solución también puede ser representada como:

\[y(t)=Asen\left(\sqrt{\frac{k_{1}k_{2}}{(k_1+k_2)m}}t+\phi\right)+\frac{mg(k_1+k_2)}{k_{1}k_{2}}\]

Ahora realizamos la comparación de la gráfica de espacio vs tiempo ($x vs t$), para poder ver las diferencias:

Vamos a ver cuál es el cambio en la gráfica, en comparación con el el movimiento de un único resorte dejando fijo $k$ (gráfica color negro) y $k_2$, $k\neq k_2$ tenemos en cuenta tres casos:

1)$(k_1>k_2)<k$

2)$(k_1=k_2)\approx k$ (Acá no se sobrepone la curva si los valores de $k_1$ y $k_2$ igualan a $k$, esto es porque empieza desde un punto inicial mas cerca al origen que el resorte con constante $k$)

3)$(k_1<k_2)>k$

Además es posible generalizar el resultado si tenemos $n$ resortes en serie, así la solución toma la forma:

\[y(t)=Asen\left(\sqrt{\frac{1}{m}\frac{1}{\sum_{n=1}^{n}\frac{1}{k_{n}}}}t+\phi\right)+mg\sum_{n=1}^{n}\frac{1}{k_{n}}\]

Comentarios

Entradas populares de este blog

¿Cómo son las ecuaciones de Euler-Lagrange para un sistema de dos resortes y una masa con gravedad? (Resortes en Paralelo)

Si has estado leyendo el blog, te has dado cuenta que vamos desarrollando problemas cada vez más complejos, aunque algunas veces estos se puedan reducir a problemas más sencillos, lo unico diferente que realizamos en estos ejercicios que tienen esa ventaja es presentar el lagrangiano del sistema, los puntos clave de la solución, así como una breve interpretación; en este caso tenemos dos resortes que sostienen una masa, con gravedad: Si te preguntas cuál es la coordenada generalizada para este problema, pues debemos recordar que es aquella por donde se realiza el movimiento, y el movimiento en ambos sistemas se realiza en el eje $y$, ahora si podemos formular nuestro lagrangiano de la siguiente forma: \[L=\frac{1}{2}m\dot{y}^{2}-\frac{1}{2}k_1y_1^{2}-\frac{1}{2}k_2y_2^{2}+mgy\] Comparando con nuestro sistema desarrollado con resortes en serie , en esta ocasión se efectua una energía potencial total de los resortes, igual a la energía que contribuye cada resorte a la masa. \[...

¿Cómo son las ecuaciones de Hamilton y el espacio de fase para un oscilador armónico en una dimensión?

Esta vez, veremos como es la forma de las ecuaciones de Hamilton, más su solución (de las ecuaciones de movimiento), y además veremos como es el espacio de fase para el resorte en su movimiento armónico. Anteriormente vimos como calcular el hamiltoniano a partir del lagrangiano, lo único que debemos reconocer es el potencial y ya estamos listos para el siguiente resultado: \[H(p_x,x)=\frac{p_{x}^{2}}{2m}+\frac{1}{2}kx^{2}\] Obtenemos las ecuaciones de Hamilton para el problema: \[\dot{p_x}=-\frac{\partial H}{\partial x}\] \[\dot{p_x}=-kx\] \[\dot{x}=\frac{\partial H}{\partial p_x}\] \[\dot{x}=\frac{p}{m}\] De la primera de las ecuaciones de Hamilton se puede obtener la ecuación diferencial del oscilador armónico unidimensional: \[m\ddot{x}=-kx\] Dividimos por $m$ e igualamos a cero: \[\ddot{x}+\frac{k}{m}x=0\] con $\frac{k}{m}=\omega^{2}$ (frecuencia angular)$^{2}$ y llegamos a la ecuación del movimiento: \[\ddot{x}+\omega^{2}x=0\] La solución para está ecuación dife...

¿Cómo son las ecuaciones del movimiento para un resorte en paralelo con el formalismo de Newton?

La idea de mostrar primero, un sistema de dos resorte con gravedad como en la publicación anterior, es para visualizar mejor, como sería un sistema de dos resortes en paralelo (sin gravedad), y que se mueve a través del eje horizontal: Ahora sí podemos formular nuestra suma de fuerzas que actúan sobre la masa: \[\sum F_x: ma=-k_1x_1-k_2x_2\] Comparando con el problema en serie la fuerza total es igual a la suma de las fuerzas: \[F=F_1+F_2\] Pero $F=-kx$: \[-kx=-k_1x_1-k_2x_2\] Pero como la distancia recorrida es la misma, tenemos el valor de la constante del resorte equivalente: \[k=k_1+k_2\] Es así como la sumatoria de fuerzas en términos de la constante del resorte equivalente, queda de la forma: \[\sum F_x: ma=-kx\] Que corresponde a la ya solucionada ecuación diferencial del oscilador armónico en una dimensión : \[\ddot{x}+\frac{k}{m}x=0\] \[x(t)=Asen(\omega t+\phi)\] Con $\omega=\sqrt{\frac{k_1+k_2}{m}}$. Aunque la solución tenga el mismo procedimiento, y aparentemente la mi...

Solución Física

Buscar este blog