¿Cómo son las ecuaciones de Euler-Lagrange para un oscilador armónico con gravedad en una dimensión?

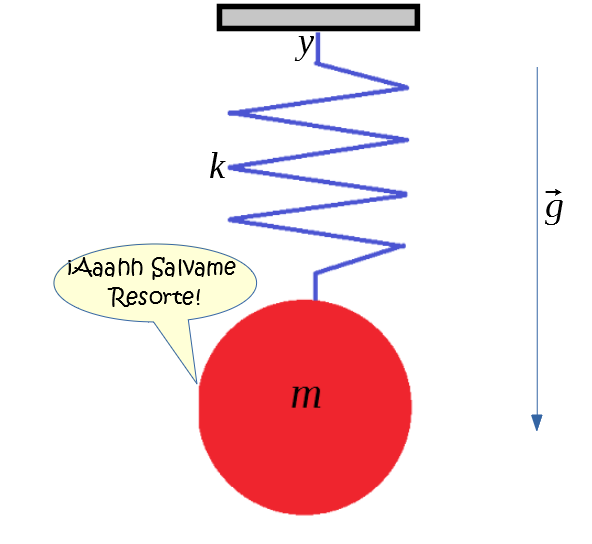
Es el turno de aplicar las ecuaciones de Euler-Lagrange para nuestro sistema de resorte con gravedad:

La energía cinética de la masa es $T=\frac{1}{2}m\dot{y}^{2}$ y la energía potencial corresponde a $V=\frac{1}{2}ky^{2}-mgy$, el lagrangiano para este caso es:
\[L=\frac{1}{2}m\dot{y}^{2}-\frac{1}{2}ky^{2}+mgy\]
Calculamos las ecuaciones de Euler-Lagrange:
\[\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{y}}\right)-\frac{\partial L}{\partial x}=0\]
\[\frac{d}{dt}\left(\frac{\partial}{\partial \dot{y}}\left(\frac{1}{2}m\dot{y}^{2}-\frac{1}{2}ky^{2}+mgy\right)\right)-\frac{\partial}{\partial y}\left(\frac{1}{2}m\dot{y}^{2}-\frac{1}{2}ky^{2}+mgy\right)\]
\[\frac{d}{dt}(m\dot{y})+ky-mg=0\]
\[m\ddot{y}+ky-mg=0\]
Que si dividimos por $m$, llegamos a la ecuación diferencial siguiente:
\[\ddot{y}+\frac{k}{m}y=g\]

Que puede ser representado en la forma (Esto porque $\frac{k}{m}=\omega^{2}$):

\[\ddot{y}+\omega^{2}y=g\]
Y la solución para está ecuación diferencial corresponde a:
\[y(t)=Asen(\omega t+\phi)+\frac{g}{\omega^{2}}\]

También representada como:

\[y(t)=Asen(\omega t+\phi)+\frac{mg}{k}\]

Esta solución corresponde a la trayectoria que menos genera energía para nuestro problema.